Jeremy Silman plays Nations

I played my 6th game of Nations last night, and in the ensuing discussion I wound up thinking about Jeremy Silman. Back when I played Chess (semi-exclusively), his book “How to Reassess your Chess” did very well, mainly because it rhymed. But also because he presented things clearly to amateur players. The most interesting idea was on exploiting imbalances.

Nations is a game of exploiting imbalances.

You can have lots of coal, or coins, or wheat. You can have little. You can have great production, or not. Military: Big or Small? Earn VP during the game or via buildings/wonders? Etc. You can’t beat everyone everywhere; you must choose your imbalances.

If you have great coins, that means you can afford the high-ticket items, so you can afford to take a few turns to get architects (for example) and pay a premium for better stuff. Or you can buy the cheap stuff, then snag a few expensive things later on. If you are coin-poor, you need to get the most important thing. If you have lots of coal, you can move people around to optimal places. You can also presumably afford to move to a high military for a turn, planning on abandoning it if necessary. (A coal poor person would be forced to keep it, since he couldn’t afford to move the workers around). A small military person may have to recognize that and boost stability (or preemptively buy a war) to avoid losing to much.

There are lots of specifics (and I’m vaguely tempted to write a few thousand words about them, but perhaps later). But the basic ideas are simple, and apply to many games:

1. Be Flexible. If you put yourself in a position where you need to grab some card, you can be screwed.
2. If you are going to be losing one type of fight (and you are), then make sure that isn’t a critical fight for you. If you are going to lose a war, by god, lose it. No point fighting for 6 grain on a crappy building if you need 7. Take the hit and boost your books and VP to compensate.
3. If everyone is fighting for resource X, then there is some resource Y they are ignoring. If you corner the market in it, they’ll all fell the pinch.
4. Having a ton of resources and few gained VP by the middle game is often just fine.

 

Sometimes not even Money …

Continuing on a tangent from actions versus words, sometimes you can’t even trust actions … if the resource in question varies dramatically from time to time. They obvious example is high stakes no-limit poker. If you (and your opponent) each have a million dollars in chips, then a $100 call pre-flop basically means your opponent has two cards (because of implied odds) But if your opponent calls $10 when you each have $20, that’s a good hand (or bad opponent).

Cylons won’t do anything out of the ordinary for small stakes. But again, that’s because this turn may be mild influence on a skill check and waiting gives the chance to make a crushing decision. Uneven resources. But in Bang! (to continue the discussion), one turn is (usually) one shot. Resources don’t vary, so you can trust actions.

Money Talks, BS walks

A few weeks ago Ta-Nehisi Coates had a guest blogger (Ayelet Waldman) talking about her experiences at a summer conference of the Army War College’s National Security seminar. This was an interesting read (and Ta-Nehisi’s blog is wide ranging, well written, and erudite). I remember hearing about (not playing) the National Security Games at Origins, and I started mentally thinking — if the National Security Seminar asked me to offer them a game to teach national security, what game would I offer?

Not a war game. I’d never be so brash as to assume that I could teach them about tactics, logistics, operations, strategy, fog of war. And my target audience probably doesn’t need this, but I think a broad swath of America (some of whom would be at the Army War College) could use a (good game of) Bang!

In Bang! (he wrote, on the off chance that non-gamers read this), you have a hand of cards, the most basic are “Bang!” and “Missed.” You can shoot whoever is in range (sitting next to you at the table if you have a pistol, longer range if you have a rifle. Some cards give you stuff, beer let’s you heal (this is a spaghetti western, after all).

The real trick of the game is you have a role. There’s the Sheriff. He wins if the outlaws and renegade are dead. The deputies win if the sheriff does. The outlaws win if the sheriff dies, and the renegade wins if he’s the last man standing (which means that he has to kill the sheriff last. The renegade is in a tough spot).

Everybody knows who the Sheriff is, but the other roles are hidden (revealed on death).

And here’s the thing — Accusations fly “Oh, he’s so-and-so.”  “He could be the renegade.” “I’m just shooting him to keep him honest.” And people pay attention to this crap. Most of the time it’s completely easy to tell someone’s motivations (with the exception of the renegade), but the information you gain from someone’s words (as compared to their action) is — nothing.

Words don’t win (or lose) the game. Actions do. A good player makes actions count. A clever player will also try to confuse things (to his benefit) with whatever words he deems most helpful, but actions have a cost (you 0nly get one “Bang!” card a turn, you only draw so many cards). Sure, sometimes a player mis-plays, but there you go. (Bang isn’t, of course, the best game to teach words versus actions. BSG is excellent, because actions are less easily interpreted. Poker is good. You can win with table presence, but great players can play without it. But poker’s too well known to make a good teaching game).

But even though there are better games for teaching this, Bang’s an excellent example, because it roughly simulates the US position at the beginning of every recent war. We’re the sheriff. Everyone knows who we are.  We have initiative (first turn) and resources. And we’re sitting a table with 4-6 others claiming to be our friends, most of whom want us dead. Some of them are in a position to do something about it, some aren’t. Your turn.

In my last game of Bang I knew everyone’s role after the first turn. By my first turn, I explained things to the Sheriff (I was deputy). But I had one huge advantage that a real world commander doesn’t. I know the exact breakdown of roles (so many deputies, so many outlaws, one renegade). The “US Army War College” version of Bang would have one sheriff (picked randomly) and then a deck of cards that includes deputies, outlaws and renegades (plural). In the real world, you don’t know exactly how many enemies you have.

(That’s the main flaw of BSG as well, two cylons in a 5 player game. If it could be 2 or maybe sometimes 3, imagine the tension when two are revealed. Of course, it would be a bitch to balance).

Anyway, once you grok Bang, then the basics of BSG, Shadow Hunters and other games become easy — follow the money, ignore the chatter. Sure, it may be helpful, but it may be intended to deceive, and until you’ve seen someone expend resources, you’ve no idea which team they are on.

Actually, I suspect most soldier’s know this lesson pretty well. I really just want to get this across to voters, who seem to be taken in regularly (about once per election).

Misc Thoughts and Links

OK, I tweeted the problem, but the long form:

Alice secretly picks two different real numbers by an unknown process and puts them in two (abstract) envelopes.  Bob chooses one of the two envelopes randomly (with a fair coin toss), and shows you the number in that envelope.  You must now guess whether the number in the other, closed envelope is larger or smaller than the one you’ve seen.

Is there a strategy which gives you a better than 50% chance of guessing correctly, no matter what procedure Alice used to pick her numbers?

I saw this a few weeks ago, and my answer was “Hell no.” I was wrong.

I don’t entirely trust New Scientist (they have a bit too much woo), but their article that some algae have been found to use quantum processes isn’t entirely new. (I remember reading Penrose’s book about that a decade ago … and Anathem last year).

In my general quest to read up pop (and real) psychology on decision making, I’m going through Ariely’s Predictably Irrational. I recommend it (in general, I recommend all books that make people consider their own prejudices and blind spots), but one story jumped out at me. (Paraphrasing): A psychologist had kids playing football outside his window, so he went to them and told them how much he enjoyed watching the play, and paid them each a dollar. The next day, he did the same thing, but only paid them 50 cents each. Each day, he lowered the amount he paid, until they finally said “We’re never playing here again!”.

Satisfied, the psychologist went back to his office and enjoyed the quiet. He’d turned their game into a job, (changing why they’d played from “for enjoyment” to “for money”) and then made sure it was a crappy job.

The (probably apocryphal) story reminded me why I never wanted to blog “professionally” (and why I resisted all urges to own a game store, etc etc).  (I may use that excuse if I never finish my Homesteaders article).

Just lucky, I guess

Here’s a bridge problem for you (not for Jeff, but the rest of you).

AQT86
AQ3
Kxx
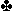Kx

KJ975
542
AQx
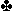Ax

You wind up in 6 spades, only to discover the unlucky duplication (both hands are 5-3-3-2 distribution). LHO leads the diamond jack (strongly hinting at the ten and probably 9). Trumps break 2-1, everyone follows suit, and your opponents are experts.

I recently discovered an article on the psychological differences between (self-described) lucky and unlucky people. The experimenter couldn’t find any actual difference (testing via picking lottery numbers, and the like). Then he asked the subjects to count the number of photographs in a newspaper section.

On average, the unlucky people took about two minutes to count the photographs whereas the lucky people took just seconds. Why? Because the second page of the newspaper contained the message “Stop counting – There are 43 photographs in this newspaper.” This message took up half of the page and was written in type that was over two inches high. It was staring everyone straight in the face, but the unlucky people tended to miss it and the lucky people tended to spot it.

After reading that I was instantly reminded of Victor Mollo’s classic introduction to card play at bridge. “Card Play Technique: The Art of Being Lucky.” Look back at that hand … anyone can make the hand if LHO has the heart king. You pull trumps, and finesse the queen. If LHO has the king, you are lucky, and if RHO has it you are unlucky.

But the winning player will notice something else. If you get rid of the minor suits, you have additional chances. Pull trumps, and run the minors. New lead low towards the queen. LHO plays the 9, so you … play the Ace! If the finesse works, you’ll still have to lose one heart anyway. Come back to hand with a spade and lead low towards the queen. LHO plays the 6 this time (see below), you play the queen, and RHO wins with the King.

But he doesn’t have any more hearts to return, and leads a club, giving you a ruff and sluff for the last trick. So, the lucky player wins when RHO has a stiff King doubleton king. What if he had Kxx (or more?) Then everyone looses. I’m not sure if being open-minded and having a positive attitude will help your luck in games, but doggedly working towards your goal with a closed mind probably hurts (as in life).

And why did the expert play the 9 of hearts on the first round? If he’d played the six, you could have just ducked in dummy. Then either RHO would be forced to overtake (and either lead a heart into the AQ, or give you that ruff and sluff), or he would show out, and the finesse would be marked. He avoided giving you a sure play, and gave you a chance to go wrong. If you didn’t, he can legitimately gripe about bad luck….

Examing gamespace via candidate moves

Computer Chess involves two algorithms.

1. Evaluate a position
2. Identify “Good” moves

The latter are called “Candidate moves.” Once you write a program to do both, you are (basically) done. On your turn, identify candidate moves, then for each candidate adjust the position, apply opponents candidates moves, and min-max. Obviously this brushes a lot under the rug … evaluating a position is not easy, either.

Most games will only have one best move in a position, but there could be a large number of good moves that are slightly inferior to the best move (and it may be beyond a players ability to determine what is best). And not all games will have a single best move at each point. (Games involving bluffing, simultaneous decisions, auctions, and other elements can confuse the mix).

Poor games widen the gap between first and second. A consistently inferior move is annoying, especially if its an ‘inorganic’ move. For example, a Puerto Rico Building that is grossly overpriced and never useful. A game chock full of those is one to avoid.

This is a roundabout way of continuing the ongoing discussion about a single way to win. Consider Puerto Rico (which I have iconoclastic thoughts on, remember). Even though I consider it an optimization game, almost every decision present several reasonable candidate moves. Almost every building shows up (not every game, but you don’t see a chess player capturing a lagging pawn with his queen for a long term sacrifice … but it shows up in World Championship play once in a while. (I don’t remember the exact players, but the game was from the ’53 candidates tournament, written up by Bronstein).

Not every move has to be tough, but not every move should be formulaic. A reasonable chess game has 40 moves (say) and if you know openings to ~8 moves, and you have a few forced exchanges and routine moves, then say you have 25 moves. (And the openings still have choices, but more stylistic). In Puerto Rico you have perhaps 12 role selections, plus building and shipping (and fields). Granted, some percentage of them will be obvious (most shipping, most fields, some buildings and roles) but you still get a good number of moves.

Le Havre? 42 moves (in a three player game) plus some building decisions and loan pay backs. But the number of moves where I feel there are multiple reasonable decisions feels much lower. Typically I stop with about 3 rounds at the end and plot my final 7-8 moves as one clump (allowing for some disruption for timing as a contingency). The opening is often “Take the best stack” or “Build a building” or “Occupy the marketplace.” Since often 1-2 of these are not valid moves, its simple.

St. Pete also seems to have a large number of automatic moves. (Again, without the expansion). One point is that If I have the wrong evaluation function (“Moving Knights never works”) then I may discount valid candidate moves. Tom explicitly mentions that possibility in his comment regarding groups with a single strong player. See Point C in this comment). I suppose, with Le Havre, that could be the case, but I rarely have to tank in Le Havre.

There’s another interesting option … a game may have one clearly best situational move based on position, but evaluating positions (not moves) may be difficult to discern without enough experience. (Or may simply be impossible in a reasonable amount of time). War of the Ring strikes me as the ‘best’ example of this, although it isn’t perfect. But even in a game like this, you have the delight of evaluation, then once you are done you simply pick the best move based on your condition. Consider St. Pete, if you mainly decide when to shift from economy to VPs, as an example.

Back to computers — they do candidate moves by a set of rules. A chess computer should consider all moves that capture, all checks, and any move that sets up a threat (I believe a common algorithm looks at the first move and assumes that your opponent passes … would your second move be brutal? If so, it’s a candidate).

I’m told that an advance in Go AIs is the idea of just selecting moves and then doing a monte-carlo simulation of the position (randomly playing pieces) and that that works reasonable well for ‘strategic’ placements (not for tactical fighting, of course).

In a new game, I’ll cycle through all the options and then pick. But as I get better, typically I’ll just focus on a few candidates and explore them deeply. This is (apparently) typical. If I play well, I’ll ‘automatically’ (ie, intuitively) pick the reasonable candidates. Of course, I can miscalculate or have a blind spot.

The “One way to win” games may be interesting or not. In Puerto Rico, evaluating the position and the ‘look ahead’ features are difficult. For Le Havre? Not so much. Automobile? I’m playing less intuitively, so its an open question, but my gut is that the space isn’t too deep. St. Pete took lots of games, but I don’t pause to weigh multiple candidate moves often…

Anyway, just another way of stating and viewing the issue…

Dice Chess and the modern Euro

I first saw David desJardin’s “Dice chess” on r.g.b, I think. For those who haven’t heard of it, it has the following rules.

1. Play a game of chess
2. Both players roll a die, the winner of the chess game gets to add +1 to his roll.
3. Hi roller wins.

This came to mind when I was playing Hanging Gardens again (after playing it once a year ago). Hanging Gardens has the clever spatial building mechanic to build towers, but then the reward for building a tower is a tile draw and tiles score via set collection. Sometimes a cheap tower gets you a great tile, sometimes a great tower gets you nothing. Pretty random. You also have a card draft and sometimes the last player will always get an OK tile, and sometimes the first player gets nothing good.

All the skill gives you a bonus on your die roll. To be fair to Hanging Gardens, skill probably gives you +2.

Coupled with some cards that practically guarantee a tile versus terrible cards that can barely be played, I really should hate this game instead of being lukewarm towards it.

Now, I can understand the appeal of the luck … people with poor spatial grasps have trouble with this game, and would get pummelled if you just scored some formulae for how big each section you built was. Still, it feels hacked on. I don’t see how you can categorize a game as dice chess and like it.

Rational Agents should Win

I don’t know if I’ve linked to Overcoming Bias before or not. It doesn’t deal with gaming, but is interesting and sometimes deals with tangential items of interest (especially to game theory).

Today they are talking about Newcomb’s Paradox (which I first encountered in a math class in middle-school. Thanks, Martin.)

And the following jumped out:

Nonetheless, I would like to present some of my motivations on Newcomb’s Problem – the reasons I felt impelled to seek a new theory – because they illustrate my source-attitudes toward rationality. Even if I can’t present the theory that these motivations motivate…

First, foremost, fundamentally, above all else:

Rational agents should WIN.

Don’t mistake me, and think that I’m talking about the Hollywood Rationality stereotype that rationalists should be selfish or shortsighted. If your utility function has a term in it for others, then win their happiness. If your utility function has a term in it for a million years hence, then win the eon.

But at any rate, WIN. Don’t lose reasonably, WIN.

{I’m adding them to the blogroll and cleaning up some old URLs).

Another interesting idea — Alien Problems

I saw this poker article and thought “That’s a generally applicable idea.”

You would’ve called there, right, Matt? …

My response to this question is, yes; if I had somehow found myself in that situation, I would’ve called. But the only way I could’ve ended up in that situation is if I had fallen out of a spaceship and been flung into my seat

…

I call problems like [that] “alien problems.”

Games rarely so clean cut, but it’s still a good idea: Is your current situation the result of a poor decision earlier? Focus your strategy thoughts where they matter.

[Hat Tip: Fourth Checkraise]

Broadly applicable strategic ideas

So, I chimed in on a San Juan strategy thread … and it got me thinking.

During the conversation I describe a situation of implicit collusion. I first heard this mentioned in Lee Jones excellent book, Winning Low Limit Hold’em. But the idea is certainly more general than poker.

Since I play a large variety of games, it’s useful to generalize. So I use it to mean “A situation where the other players, by their sheer number, stand as a deterrent against one or more strategies.” The poker book used it to mean “You can’t bluff, because odds are one player has a calling.” But it goes beyond bluffing.

In particular, it’s affected my thinking one San Juan and other games. I wonder what other ideas I’ve taken (or missed) from other games or fields?

• Time Value of Money
• Prisoner’s Dillema
• Opportunity Cost
• Accepting short trades (There must be a better name for this).

And, of course, lots of probability theory, math, puzzle solving, and the like. I’m sure there must be more.

So, what strategies have you found in unexpected places?